This write-up documents the moment when I first unified several algebraic tools into a single, reproducible factorization pipeline. It is demonstrating that the chains of fallback-secure can apply the general algorithm in real time.

1. Motivation

I needed a method that would not fail when factoring cubic polynomials that appear inside rational functions.
Standard techniques (grouping, synthetic division, pattern matching) work only in specific cases.
I wanted a pipeline that always terminates, and one that reinforces my understanding of multiple tools at once.

2. Example Function

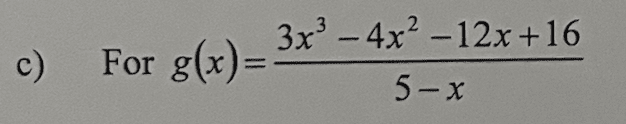
I started with the example:

$g(x) = \frac{3x^3 - 4x^2 - 12x + 16}{5 - x}$

The demand is to identify the intercepts and asymptotes, graph the rational function.

---

3. Standard Grouping Attempt

I attempted grouping first:

• Rearranging $3x^3 -12x -4x^2 + 16$
• Extracting common factors of $3x$ and $-4$
• Obtaining $(3x - 4)(x + 2)(x - 2)$

This was the “single-branch” solution: valid, but limited because it depends on the pretty equation.

---

4. Why a Pipeline Was Needed

Grouping works here, but:

• It fails for many cubics
• Synthetic division only works if the first guess is correct
• Pattern recognition is unreliable
• Quadratic factor leftovers often appear

So I needed a general algorithm rather than “whichever trick works”.

---

5. The Pipeline (General Algorithm)

The method integrates four blocks:

1. Rational Root Test
   Generate possible rational roots from (constant ÷ leading-coef).

2. Synthetic Division
   Test a candidate.
   If the division succeeds → we can get a quadratic.

3. Quadratic Formula
   Solve the remainder quadratic directly, no guessing.

4. Leading-Coefficient Recovery
   Normalize the factorization back to the true leading term.

This converts a messy cubic into a fully deterministic pipeline.

---

6. Execution on the Example

Steps:

1. RRT generates candidates like ±1, ±2, ±4, ±8, ±16, etc.
2. Testing $(x = 2)$ succeeds.
3. The remainder quadratic is $(3x^2 + 2x - 8)$.
4. Quadratic formula → roots $\frac 4 3$ and $-2$.

5. Reassemble with leading coefficient recovery:

   $3(x- \frac 4 3)(x+2)$ → $(3x-4)(x+2)$

---

7. Interpretation: Why This Works

This pipeline always terminates because:

• RRT guarantees the function eventually hits a rational zero (if one exists)
• Quadratic formula handles the remainder
• Leading-coefficient recovery preserves the original structure. Meanwhile, it can replace the A/C method that cannot handle the Leading-coef was Bigger/Odd.
• Every branch converges to the same final factorization

It is not a trick, and is an algorithm to form a unified structure for cubic factorization.

---

8. Closing Reflection

This was the first time I combined:

• [Transferring grouping method into]
• ① possible rational roots test
• ② synthetic division
• ③ quadratic formula
• ④ coefficient recovery [into a single algorithm].

The point is not efficiency, but it has to master all methods to converge for a structure chain.

This document is preserved as the first “pipeline” that I built from college-algebra materials.

Posted on: 12/03/2025

Genhai Yu

I worked in IT industries that have payment, cloud computing, telecoms, and education. Most of my responsibilities were modernizing and refactoring the legacy frameworks of the architecture. Code development and problem-solving are my interesting points. My career experience CV.