I would like to refactor this rational polynomials after seen the grouping method many times. Therefore, I built a factorization pipeline while solving a real problem in college algebra.

The refactoring steps are simple:

• Refactoring grouping method by utilizing the polynomial tools.
• Always execute this universal pipeline and do not rely on a “pretty” equation.

1. Mapping the Algebra Tools

There is no single-chain algorithm to combine all the tools for the arbitrary polynomials, and means that we choose which path works when we are solving it.

Thus, I need a factorization algorithm to stabilize the solving path for any polynomials inside the rational functions or not as a clear integer.

1. Synthetic division is not used to finish the factorization, and the function is to remove the power layer until the quadratic form we have obtained.
2. The A/C method cannot handle arbitrary leading coefficients well, especially when they are not clean integers.

2. Example Function

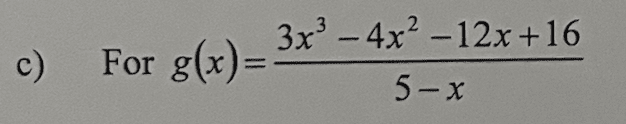
I started with the example:

$g(x) = \frac{3x^3 - 4x^2 - 12x + 16}{5 - x}$

The task is to identify the intercepts and asymptotes, graph the rational function.

Before graphing, the numerator must be factored.

3. Grouping Attempt

I tried grouping first due to the pretty equation.

• Rearranging $3x^3 -12x -4x^2 + 16$
• Extracting common factors of $3x$ and $-4$
• Obtaining $(3x - 4)(x + 2)(x - 2)$

Meanwhile, I also provided the end-behavior and graph solution.

But we can see the grouping method is to demonstrate here is a pretty equation for solving the demand.

4. The Pipeline for Refactor the Grouping (General Algorithm)

The solution was to utilize several tools and combine into one chain.

1. Rational Root Test
   Generate possible rational roots from (constant ÷ leading-coef).

2. Synthetic Division
   Test a candidate from possible rational roots until we get a quadratic form.

3. Quadratic Formula
   Solve the remaining quadratic directly.

4. Leading-Coefficient Recovery
   Restore the original leading coefficient.

5. Execution on the Example

Steps:

1. Rational Root Test produces candidates: ±1, ±2, ±4, ±8, ±16, …
2. Testing $(x = 2)$ works.
3. The remainder quadratic is $(3x^2 + 2x - 8)$.
4. Quadratic formula gives: $\frac 4 3$ and $-2$.

5. Recover the leading coefficient:

   $3(x- \frac 4 3)(x+2)$ → $(3x-4)(x+2)$

6. Repeat Why the General Algorithm is Better

• Avoid the A/C method in this scenario.
• Avoid the grouping method.

Those are the single branch method, and it is not a universal pipeline.

7. Conclusion

This pipeline of algorithms has to combine all the polynomial tools for one single chain.

• ① possible rational roots test
• ② synthetic division
• ③ quadratic formula
• ④ coefficient recovery

This method is not efficient, but it practiced the maps of algebra in my mind.

Posted on: 12/03/2025

Technical notes include mathematical structures, computer science, and low-level derivative computation. - Genhai Yu